When I was in school I never learned how to use a ratio table.  You might be asking yourself, "What is a ratio table?" I started using them as a teacher and have found them to be such a powerful tool to help students see relationships between numbers with a constant ratio, think proportionally, and think flexibly about how to solve problems.  Once you learn how simple and effective they are, I think you will find them to be useful too.

Using the Ratio Table to Organize Information

Let’s start by thinking about the number of days in a week – seven.  How about the number of days in two weeks?  We can start to organize this information into a ratio table like this…

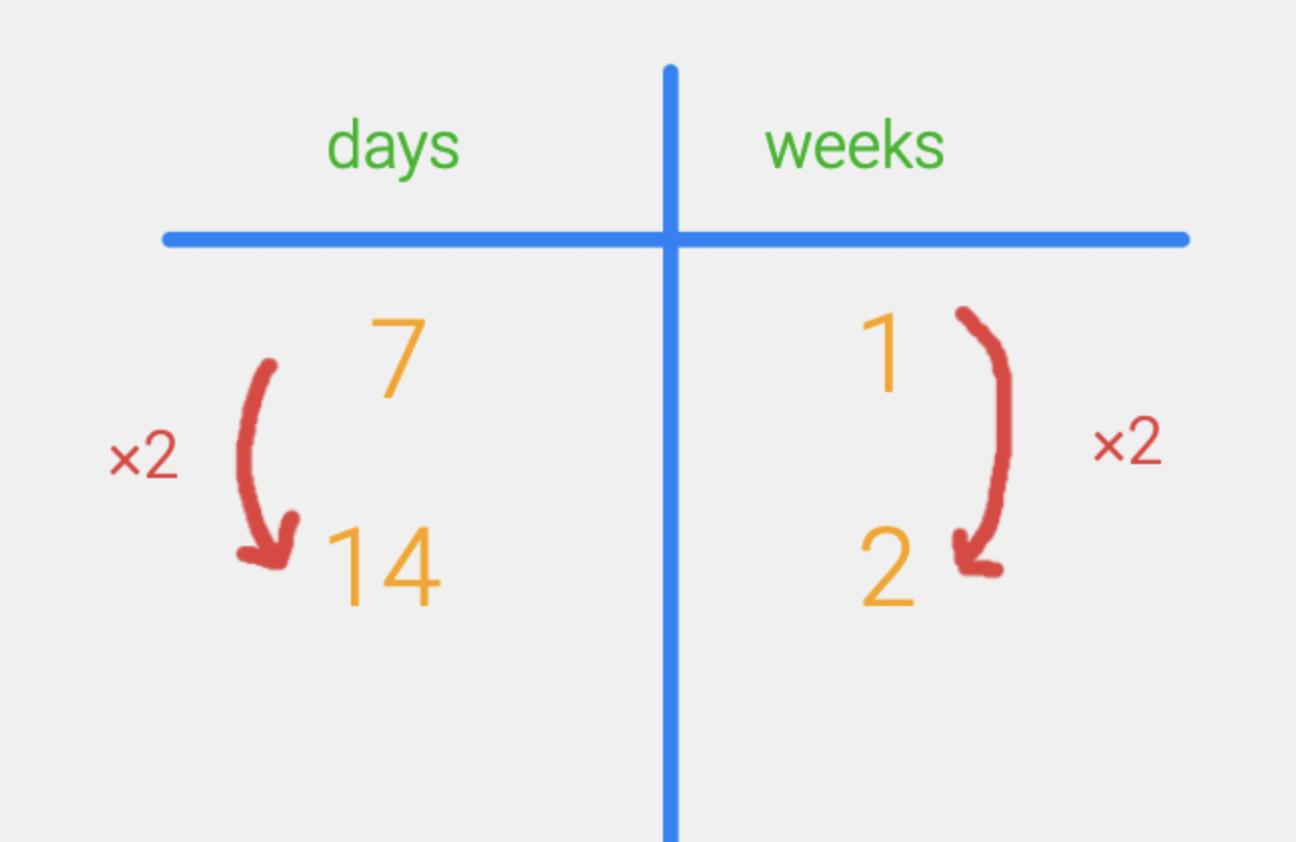
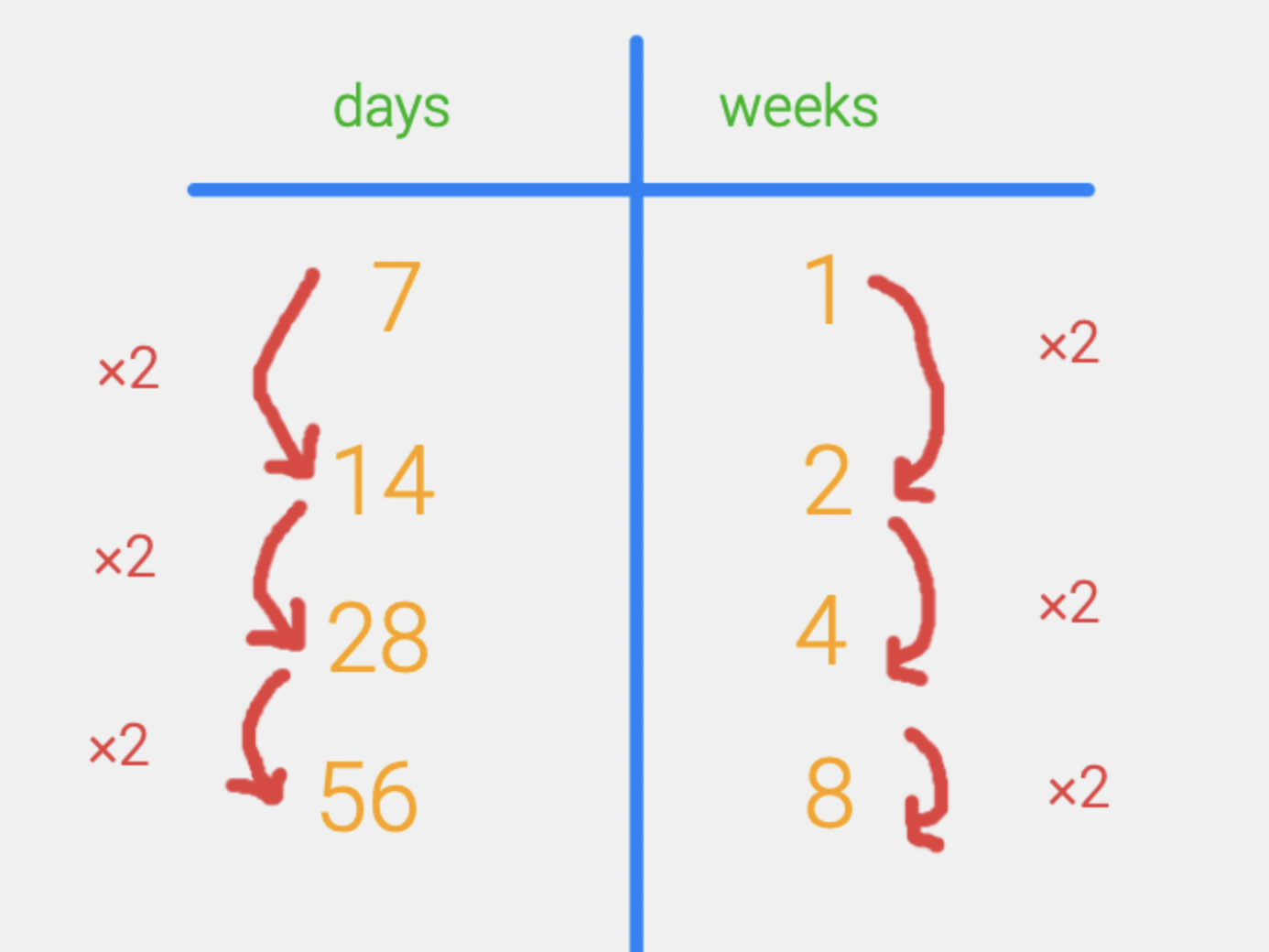
Then we can add to our table by thinking about the number of days in four weeks and then eight weeks.  Notice how we are doubling each time.  If we double on one side, then we also need to double on the other.  

Extending our Thinking to Unknown Quantities

Now what if we wanted to figure out the number of days in six weeks?  Can we use the information we already have on the table to figure it out?  We can add the number of days in two weeks to the number of days in four weeks and then we will know how many days are in six weeks.

Working Backwards to Find Other Unknown Quantities

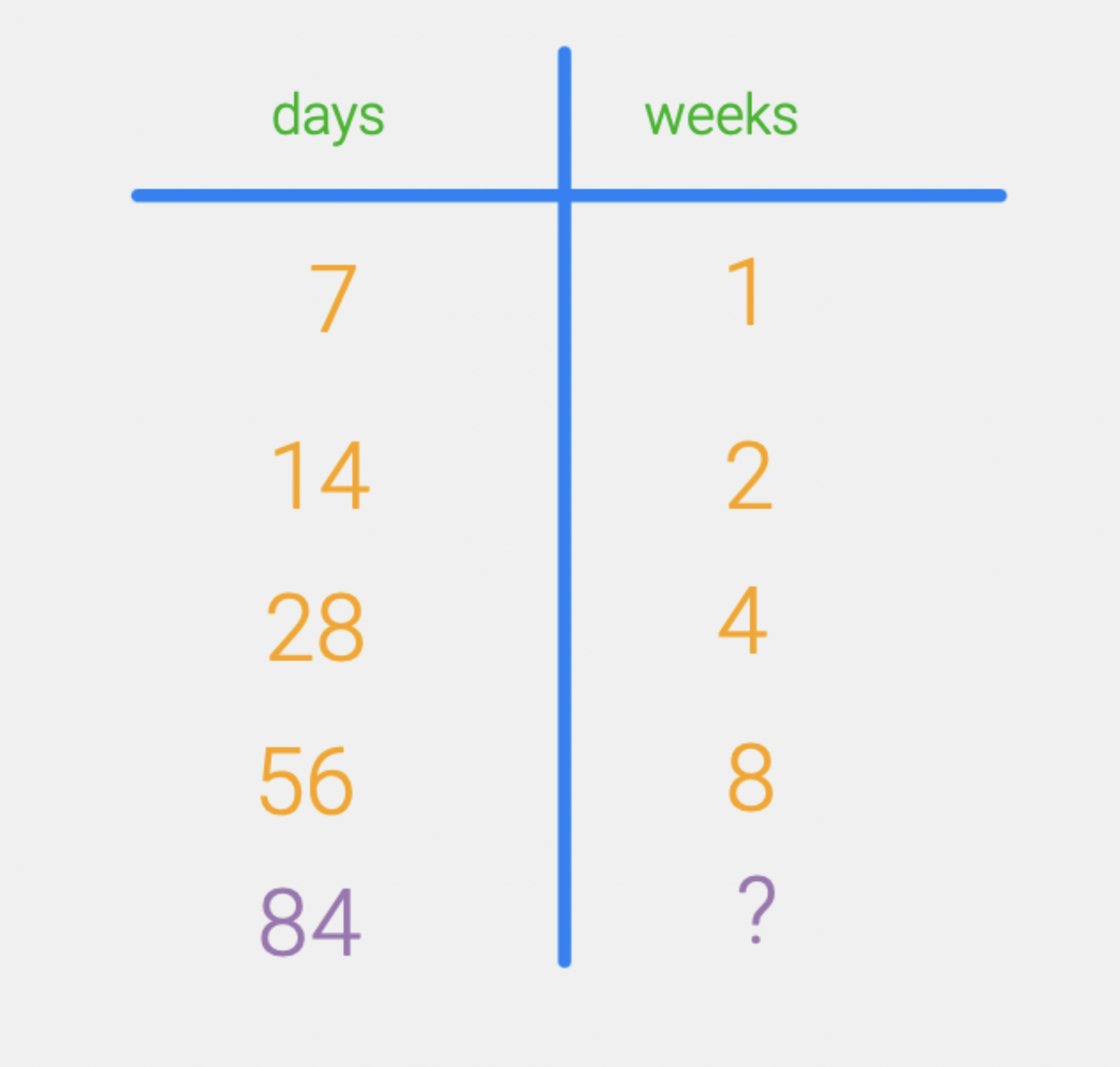
Sometimes we know the number of days but we don’t know the number of weeks.  If we knew that we had access to a TV show for 84 days.  How many weeks would that be?  Again, we can use the ratio table but this time we will work backwards to figure it out.   What can we add in the days column to get 84 days?  A little bit of thinking about the table gives us the idea that 28 plus 56 is 84 so therefore 28+56 = 84.  Since added those two numbers in the days column, we then add the corresponding numbers in the weeks column –  4+ 8 = 12.

Once you start using the ratio table, you will find more and more ways to use this tool to organize your thinking. When my daughter was younger she had to figure out how many students were attending a field trip if the cost was $351 and the tickets were $13 each. Seen as a division problem, this problem was way beyond her reach at the time but by using a ratio table we were able to work our way up, doubling as we went and then finally adding to find the solution.