Math Practice #6 “Attend to Precision” feels familiar to most of us because it feels like the math goal of a generation ago of finding the correct answer and showing our work.  This math practice, however, has a much broader meaning. We still want students to find the correct answer to a problem, and now other types of precision are recognized as valuable in skilled mathematicians as well.

Precision With Language

Children need to be able to clearly show their methods and thinking.  We want students to show how they actually solved a problem.  When asked how they solved a problem, younger children often tell me, “My brain told me.”  While this is true, we want to know what the brain said.  With a little prompting, students can often explain that they counted by twos and then added one more or the saw pictures of cats in their head and then counted the legs.  These different strategies are valued.  With some guidance students can articulate what their strategies are so that they can learn how to explain them. 

Precision With Vocabulary

Students need to be able to use precise language when discussing their work.  Do they know what an array is?  Can they give a definition, not just build an array?  Do students know what a quotient is or do they get it mixed up with the dividend?  My favorite mix-ups are with the use of polysemous words because these are so interesting and lead to some fun conversations.  Polysemous words are those that mean something in our daily life but have a different meaning in math. “Can I have some of your goldfish crackers?” implies that the child would like a few, but not all, of their friend’s crackers.  “Find the sum,” requires students to find the total of the numbers in the problem.  In this case they are looking for all of them.  These words can cause a lot of confusion for children as they are learning math, especially if they are English language learners.  (For more fun with polysemous math words, you can read my blog post here.)

Precision with Models and Sketches

When building 3D models, children also need to be precise.  If the problem is 14 + 37 then there should actually be 51 pieces in the solution. 

As children make sketches and drawings of their solutions, the same need for precision exists.  The sketch needs to match the problem and show the operation under consideration. 

This example of 65 ÷ 8 came from a group of 5^th graders.  See how one image shows the divided, divisor, and quotient?  The other image is just the equation written out with blocks.  The amounts do not have any relation to the problem.

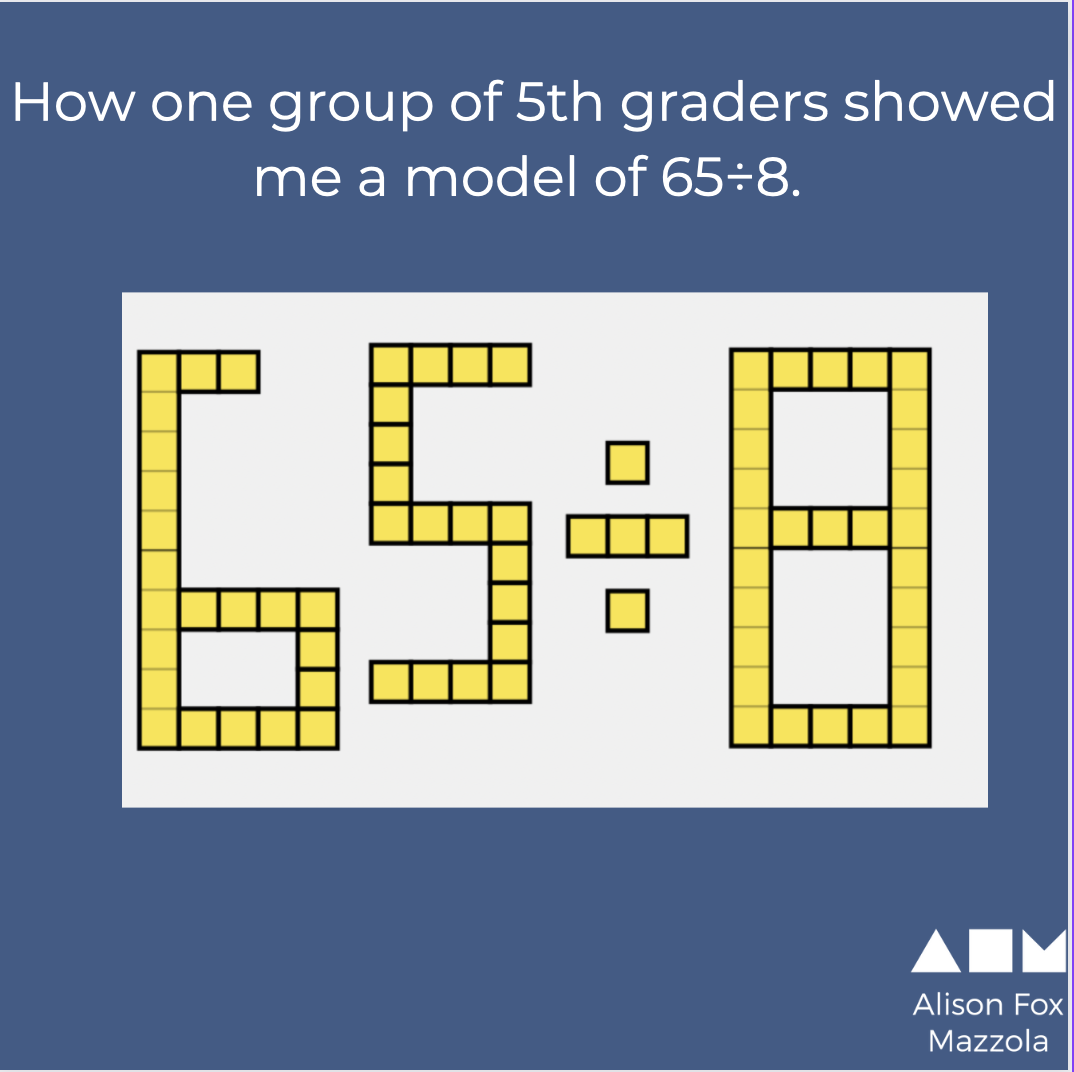
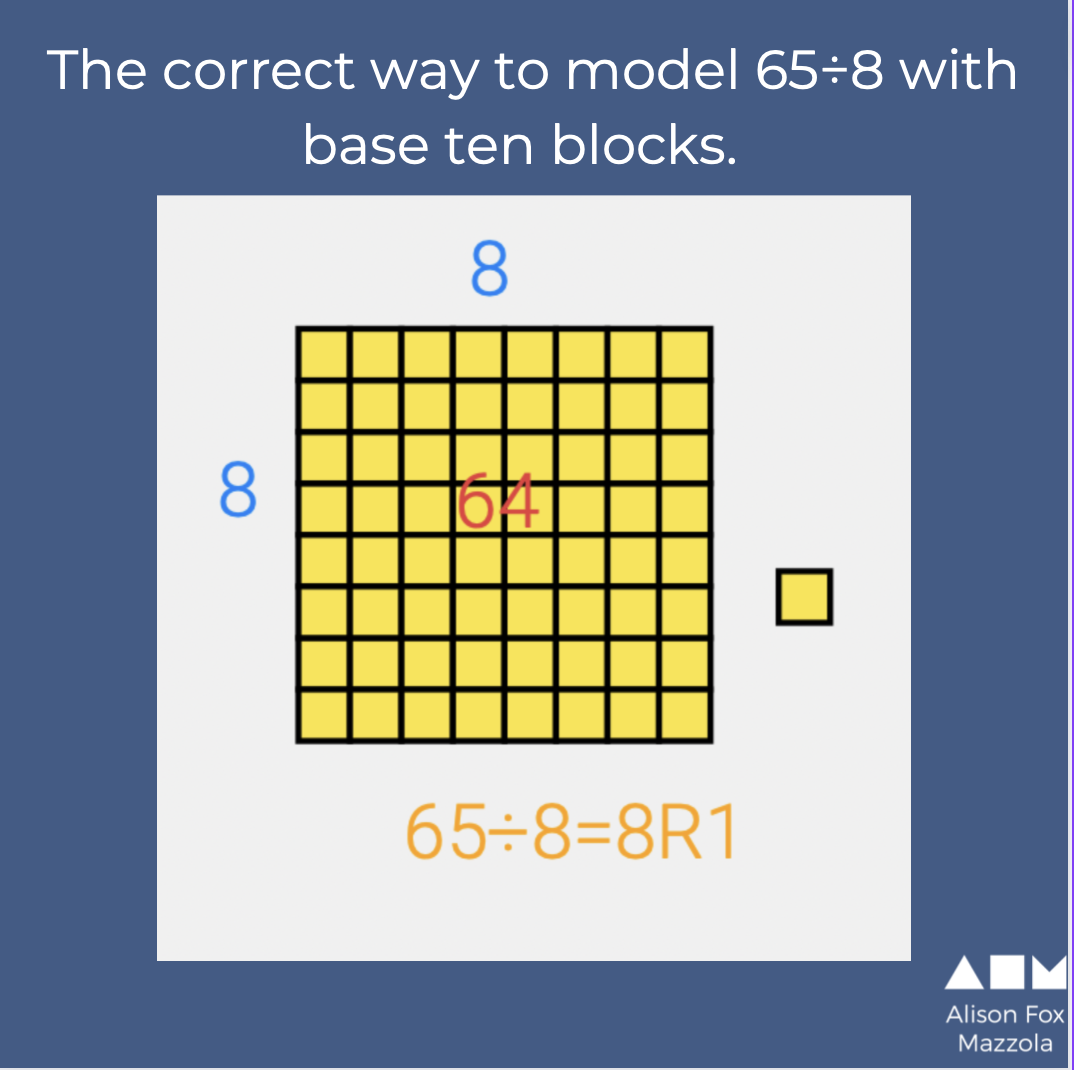
When children carefully build models or make sketches they can see the structure of the problem under consideration and see how the math makes sense.

Precision with Labels

Many, many students will focus so hard on solving a problem that they completely forget to go back to the context and add a label to their answer.  Was this problem about cars for a field trip or legs on a horse?  Reviewing the context of the problem helps students to label their answer and also to note if their answer makes sense.  I always get a laugh when 4^thgraders think we should take 6.5 cars on a field trip.  Context matters!

Labeling is also super important when measuring.  A length of 1 km is very different from a length of 1 dm.  Effective math communication requires attention to the details of labels.

Precision with Symbols

What does the equal sign mean?  Surprisingly, it means something different to many young children than you may think. Let’s look at: 

7+9 = ______ + 10

Many, many children think that 16 belongs in the open space.  Can you figure out why? 

In their minds the meaning of the equals sign is similar to “Do something.”  If they take 7 and 9 and the plus sign and are to “do something” then they come to the conclusion that it makes sense to put 16 in the empty space. 

The true meaning of the equals sign is about balance.  Both sides need to be balanced.  When children build this equation on a pan balance or build each side with cubes, they can see that 6 is the correct answer for the empty space.  This is another example of where precision with our use of written symbols and their meaning is essential in order to be able to do math accurately.

 Application in a Broader Context

Precision with language, vocabulary, models, labels, and symbols requires a much broader skill set than just finding the correct answer.  However, this precision leads to clearer written and oral communication.

Our language is full of casual terms such as “Kinda” or “Sorta.”  It takes nudging to get students to think and speak more specifically.  The effort is necessary to communicate effectively in math.  In addition, the clear logic and expression in math will lead to clear logic and expression in other areas.  This is a life skill that any employer will value.

To learn more about how to support your child in learning math strategies, vocabulary, and visual models for 2nd - 5th grade math, take my online course.